11261. Разрезание
палки
Вы должны разрезать деревянную
палку на куски. Самая доступная компания The Analog Cutting Machinery, Inc. (ACM) взимает плату в зависимости от длины
разрезаемой палки. Их порядок работы требует совершать только один разрез за
раз.
Легко заметить, что разный выбор
порядка разрезов приводит к разным ценам. Например, рассмотрим палку длиной 10 метров,
которую следует разрезать в точках 2, 4 и 7 метров с одного конца. Рассмотрим
несколько вариантов:
·
Можно резать сначала в 2, затем в 4, а потом в 7. Это приведет к цене 10 + 8
+ 6 = 24, потому что первая палка была 10 метров, вторая 8 метров,
а третья 6 метров.
·
В другом варианте сначала разрежем в 4, затем в 2, а потом в 7.
Это приведет к цене 10 + 4 + 6 = 20, что
является лучшей ценой.
Ваш начальник доверяет Вашим
компьютерным способностям определить минимальную стоимость разрезания данной
палки.
Вход. Состоит из нескольких тестов.
Первая строка каждого теста содержит длину палки l (l < 1000),
которую следует разрезать. Следующая строка содержит количество разрезов n
(n < 50), которые следует сделать.
Следующая строка содержит n
положительных чисел ci (0 < ci < l),
представляющих места для разрезов, заданные в строго возрастающем порядке. Строка
с l = 0 обозначает конец входных данных.
Выход. Выведите минимальную стоимость
разрезания палки в формате, приведенном в примере.
|
Пример
входа |
Пример
выхода |
|
100 3 25 50 75 10 4 4 5 7 8 0 |
The minimum cutting is 200. The minimum cutting is 22. |
РЕШЕНИЕ
динамическое программирование
Анализ алгоритма
Пусть массив m
содержит точки распила: m1,
…, mn. Добавим начальную и
конечную точки: m0 = 0, mn+1 = l.
Пусть функция f(a, b)
возвращает минимальную стоимость распила куска палки от ma до mb
с учётом
необходимых точек распила, находящихся внутри отрезка. Внутри отрезка
[ma; ma + 1] точек распила нет, поэтому f(a, a
+ 1) = 0. Ответом на задачу будет значение f(0, n + 1). Вычисленные значения f(a,
b) сохраняем в ячейках массива dp[a][b].
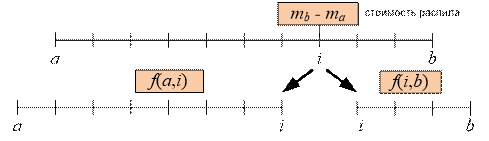
Пусть отрезок
палки [ma, mb] следует распилить на
несколько частей. Если первый распил мы произведем в точке mi (a < i < b), то стоимость самого распила составит mb – ma.
Далее следует распилить оставшиеся куски соответственно за цену f(a, i)
и f(i, b). Значение i следует выбрать
так, чтобы минимизировать суммарную стоимость:
f(a, b)
= ![]() + mb – ma
+ mb – ma
Пример
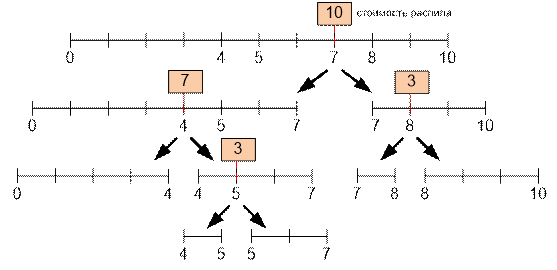
Рассмотрим второй
тест. Приведем один из возможных методов распила палки длины 10 стоимостью 10 +
7 + 3 + 3 = 23:
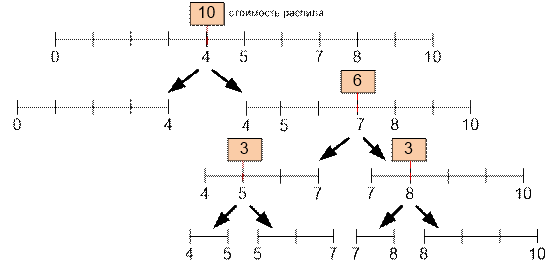
Рассмотрим
оптимальный метод распила стоимостью 10 + 6 + 3 + 3 = 22:
Реализация алгоритма
Объявим
константы и рабочие массивы.
#define MAX 55
#define INF 0x3F3F3F3F
int dp[MAX][MAX];
int m[MAX];
Функция f(a, b)
возвращает минимальную стоимость разреза куска палки на отрезке [a; b] с учётом точек распила,
находящихся внутри этого отрезка.
int f(int
a, int b)
{
Если a + 1 = b, то внутри отрезка [a; b] точек разреза нет.
Возвращаем 0.
if (b - a == 1) return 0;
Если значение f(a, b) уже вычислено,
то возвращаем его.
if (dp[a][b] !=
INF) return dp[a][b];
Совершаем разрез в точке i
(a < i < b). Вычисляем
стоимость следующим образом:
f(a, b)
= ![]() + mb – ma
+ mb – ma
for (int i = a + 1; i
< b; i++)
dp[a][b] =
min(dp[a][b], m[b] - m[a] + f(a, i) + f(i, b));
Возвращаем результат f(a, b)
= dp[a][b].
return
dp[a][b];
}
Основная часть программы. Читаем входные данные для каждого
теста.
while(scanf("%d",&l),l)
{
scanf("%d",&n);
Добавим начальную и конечную точки
распила: m0 = 0, mn+1 = l.
m[0] = 0; m[n+1] = l;
for(i = 1; i
<= n; i++)
scanf("%d",&m[i]);
Инициализируем массив dp.
memset(dp,0x3F,sizeof(dp));
Вычисляем и выводим ответ.
printf("The
minimum cutting is %d.\n",f(0,n+1));
}